本文特別提出不同的預測演算法，以及如何使用定性和定量的方法來得到一個預測產品需求的最佳框架。

在預測的領域中，沒有比預測半導體的需求更複雜，但這是一個可能讓準確預測成為一個長期生存的生意。不僅透過預測在通路持有適量庫存有助於降低公司成本， 也能得知想要建置一個當客戶在他們需要產品，能滿足他們需求的健全自適應控制系統時會缺少什麼部分，其他還有包括像改進供應商協定和最佳資源（勞動力和資本）分配的好處。

關於方法…

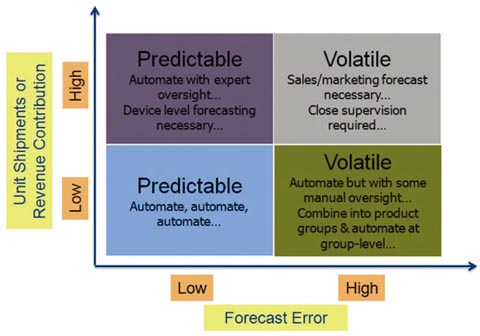
一般有兩種方法來預測基於時間的事件：定性的方法，以及定量或更多的數據為基礎的方法。如果歷史時間序列數據感興趣的變項是粗略的，或者被預測的事件事關新產品的推出，更主觀或基於專家的預測方法是必要的，我們都直觀地知道這一點。新產品的推出往往涉及現有的客戶和供應商的協定，而這讓我們容易掌控要建置什麼、何時、以何種數量。即使如此，巴斯擴散模型　—　一個旨在幫助預測銷售一個新的產品類別時，可以採用的技術將可能會被應用，但是這篇文章將不討論它。現在，如果對預測過去的變相信息數據是個很方便、可量化、以及公平的假設，過去的模式將在未來有可能繼續；那麼更多的定量化，演算法，有點自動化的方法幾乎是必然的。但是，如何決定是否使用一個自動化的方法或是多個以專業為基礎的方法？一個典型的半導體公司的產品可以被區分成四個象限（圖1） ，並取決於哪個象限的產品最適合來決定是否自動預測的過程。

圖1. 一個典型的半導體公司的產品可以被區分成四個象限

時間序列建模

一個產品過去的出貨統計數據或一組試著預測需求的產品是很常見的，而那通常就是唯一一個你需要用來設計自動產生預測過程的數據。目的是發現在歷史，時間序列數據的模式，並推斷該模式至未來發展。一個理想的系統應建立在以下的方式—若是發貨模式改變－它能發展或自我適應，並從預先建立的工具集選擇正確的演算法。一個典型的時間序列預測模型將只有兩個變項：一個獨立的時間變項和一個代表我們試圖預測的事件的應變項。

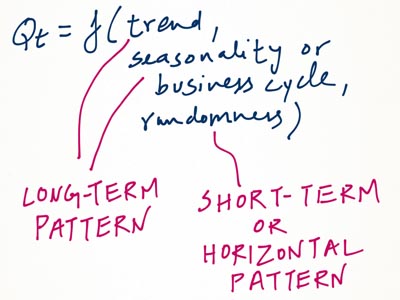
這一事件的Qt（訂單、發貨，等等），我們試圖預測的多半是產品的生命週期和趨勢，季節性或經濟週期和隨機性，如圖2顯示的功能。趨勢和季節性或商務週期通常與長程模式相關，因此最適合被用在產出長期預報。一個短期或水平模式通常是隨機的，並用於短期預測。

圖2. 事件的Qt預測圖

預測近期事件

過去的數據表現出水平模式的隨機性可以透過使用樸素法或簡單平均法進行合理預測。兩者之間的選擇將取決於哪一個給出較低平均絕對誤差（MAE）和平均絕對誤差百分比（MAPE）。

樸素法

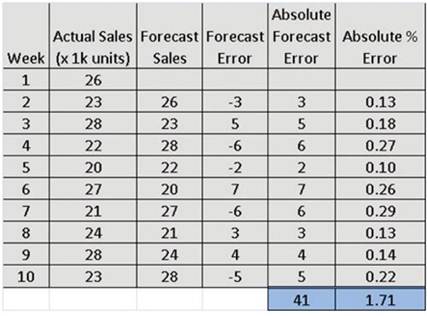
在圖3中的示例表顯示相當於十周的銷售數據。使用樸素法，第二週的預測值恰好等於第一週的出貨。第三週的預測值則正好等於第二週等實際銷售價值，以此類推。實際值和預測值之間的差別分別代表預測誤差和計算總誤差的絕對值。MAE只是總誤差的平均值。類似的方法用於計算MAPE，只是在每個獨立的誤差除以實際銷量來計算百分比的誤差，然後將其加總摒除以預測值的數據來得到MAPE。

圖3. 十周銷售數據的示例表


平均法

與其用最後一次觀察到的事件預測下一個事件，更好的方法是透過過去所有觀察所得到的平均值並用於下一個時期的預測。例如，對於第3週的預測值等於第1和第2週的實際銷售值的平均值。第4週的預測值是前三個實際銷售值的平均值，以此類推（圖4） 。

圖4


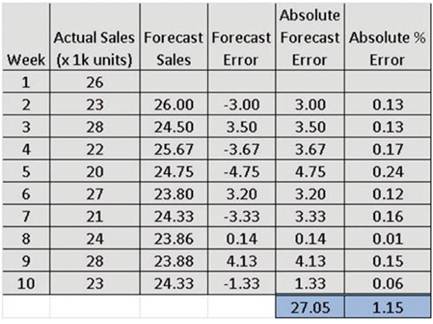
MAE和MAPE為樸素法時分別為是4.56和19%，兩者同為平均法則分別為3.01%和13% 。因此可以得出結論，平均法比樸素法更好。

階段提升的水平模式

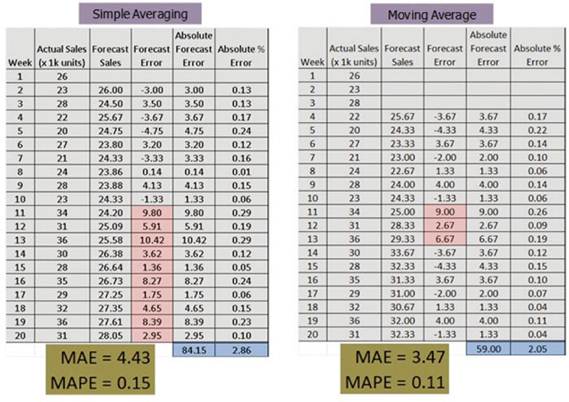
但是，當銷售模式突然發生變化（不論是否在預期內），類似圖5所示的情況會怎樣？簡單平均法將會需要進行調整，以此為出發點，移動平均法更適合。取代將整個時間序列平均的做法，只有第2或3或4個最近時間的事件被用於計算預測值。要使用多少時間段將取決於哪一個給出了最小的MAE和MAPE值，並能夠也應該參數化和編碼。圖6中的表比較這兩種方法，並明確了移動平均線似乎是一個更適合用在預測未來事件的方法。　

圖5


圖6

指數平滑法

但通常情況下還有一個更好的方法，尤其是在過去的數據表現出嚴重和隨機的水平位移。這種方法非常適合於那些因為隨著時間的推移，在整個時間序列的指數加權移動平均值趨向於淡化數據—就算比較舊，但依然包含在內，且同時加重最近事件加權的情況。實際和預測值之間的關係顯示於圖7 。

圖7

同樣的，最低的MAE和MAPE將有助於決定平滑常數的最佳值，並一如既往，很容易根據既有的數據編碼並在新數據進入時自動更新。

但基於上述的平滑方程式，我們必須知道整個時間序列是如何在只有作為下一期的預測部分研究的最近實際和預測值產生的。請見圖8中的解釋。

圖8

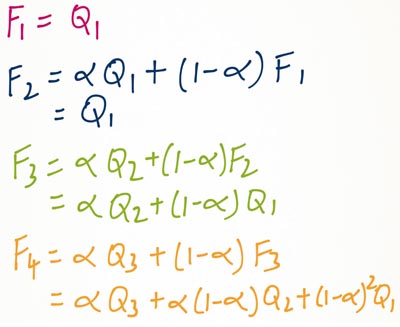
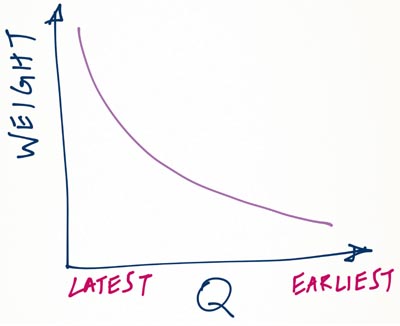
對於第二週期的預測被假定為第一觀測值。第三個時期是真正的預測得出，並與隨後的換人，人們很快發現，對於N個週期的預測是歷屆觀察事件的加權平均值。且歸於較早期事件之後發生的事件的重量示於圖9的曲線圖。

圖9

做長期預測

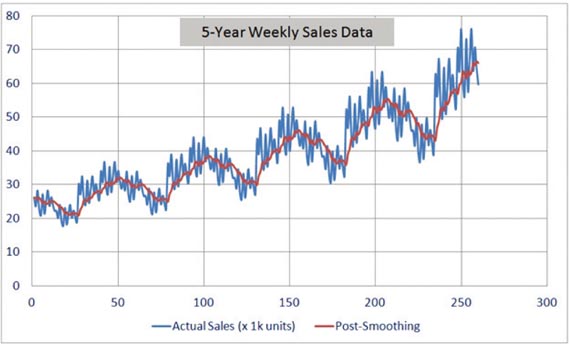
半導體產品的生命週期通常是以月為單位衡量，但也有相當少數的產品是按年計算壽命，特別是在終端應用具有長期和日益普及的週期。這些產品不僅展現時間序列的短期隨機性，多年來也表現出長期的季節／週期性的不斷增長或下降趨勢。在估計較長期之預測的第一步是修勻一些用於之前討論過的方法的短期隨機性。不修勻和修勻曲線可能類似於圖10中的情節。

圖10

顯然，數據顯示出伴隨著一個每年都重複的季節性或週期性模式的長期趨勢，而最小二乘法或迴歸分析是用以形成一個幫助估計這一趨勢及所涉參數功能的理想方法。但緊縮數字之前，該數據集必須先準備在該季節性的行為加入一組代表不同的時間間隔的二分資料變數。因為在這種情況下，該季節性是Q1、Q2、Q3和Q4做季劃分，且只有其中的三個被包括在該模型中。第四個，即是在Q = 2這種情況下，形成測量其他三季的顯著性的基礎（圖11）。

圖11

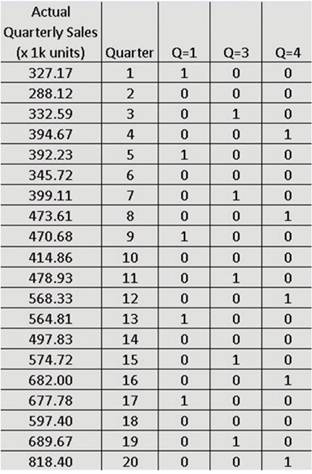
圖12

以季計算的預測值的函數形式看起來像圖12所示．截距B0的上下移動是建立於該季是否是Q2。如果B2、B3和B4是正的，那第二季將表現出預期的最低銷量。其他三季將顯示增加與相應的參數估計值與預期的銷售一致。而這個方程式可以很容易地用於合理預測將來的幾季或幾年的某一個事件。所以這說明實現自動化預報過程的某些功能有多麼容易；建立一個有智慧，自我意識和自適應預報系統有多重要。其結果不僅會降低成本，而且有助於重新聚焦供應鏈的規劃工作來迎接更長遠的挑戰。

本文經《半導體科技雜誌》同意轉載　
原文請參閱《半導體科技雜誌 SST-AP Taiwan》

【本文僅反映專家作者意見，不代表本報立場。】

Facebook 在北美智權報粉絲團上追踪我們