前言
西元1637年,法國著名的哲學家、數學家以及物理學家笛卡兒發表了「方法論」一文,該文是人類史上首篇有關於方法論的著作,對於後世的學術發展與科技昌明,可以說是發揮了啟蒙與引導的重大作用。這篇論文的主要內容包含四個部分,分別是「獨立思考」、「學習與研究」、「質疑與善問」以及「實踐」等;隨後,笛卡兒也留下了「我思故我在」的千古名言。綜觀近代產業界與學術界發展出來的各式各樣有關於「發現問題與解決問題」的方法論述,究其基本的理論架構,都不脫離開山祖師爺笛卡兒所著的「方法論」之思想範疇。
環顧現代產學界所習知的方法論當中,若要論其應用的領域與實踐的價值,最受科技業者廣泛肯定者,大概要算是前蘇聯發明家Genrich Altshuller先生所創立的TRIZ (Theory of Inventive Problem Solving),中文譯為「發明問題的解題理論」。Altshuller先生當初收集了20萬件專利文件進行分析,發現不同產業的技術發明之間,往往存在著相似的科學原理之背景,只要多運用聯想力,在類比式思考的輔助下,許多難解的技術問題都可以在其他產業中發現可改良與應用的答案。近20年來,在歐俄與美日韓地區,許多知名的大學院校都紛紛加入推動TRIZ教學的行列。以當今全球前500大企業而言,其內部的創新研發活動與製程改良改善的專案計畫,也都曾經廣泛地應用到TRIZ方法論。
1968年,Altshuller先生在前蘇聯政府的長期刁難下,終於獲得官方的同意,首度公開發表其創建的TRIZ方法論。近年,俄羅斯的TRIZ團隊將其理論架構歸納為五大部分,分別是:
- 公式化模式(Formalized problem model),內容包括TRIZ的基本概念介紹。
- 雙參數模式(Two-parameter problem model),內容包括39個工程參數,40個發明 原則和應用矛盾矩陣轉換出消除工程矛盾的特定解。
- 結構化模式(Structural problem model),內容包括應用物質與場的分析模型對應至76個標準解的便捷方法。
- 單一參數模式(One-parameter problem model),內容包括應用4種分離原則對應至40個發明原則,再轉換出消除物理矛盾的特定解。以及
- 發明問題的解題演算法(ARIZ),內容敘述解決複雜問題的9大步驟與應用。
由於TRIZ的理論體系龐大,受時間與篇幅所限,筆者必須限縮討論的範圍,故以專利檢索和產學合作的實例為前提,為讀者們做一番解析與說明。
TRIZ 應用的實例與解說
筆者初步檢視國內各大學的學術論文,發現其中應用TRIZ方法論至產業技術的相關著作,可以說是有如鳳毛麟角。所幸獲得一篇某國立大學的研究論文,該篇論文的主題是有關於半導體化學機械研磨(CMP,Chemical Mechanical Polishing)技術的演進實例,並輔以TRIZ 39x39工程參數的矛盾矩陣,40個發明原則和專利說明書的解說,不僅是國內學術界少見的代表作,其實務內容更有益於產學合作與教育訓練的推廣目的。
首先,該論文作者列舉一完全適用於矛盾矩陣之案例如下,專利名稱為”Forming a transparent window in a polishing pad for a chemical mechanical polishing apparatus(在CMP設備的拋光墊上裝置透明視窗)”,專利號碼為US5893796。
如圖一所示,該案例敘述一CMP設備在研磨墊上裝置複數個偵測窗口,利用雷射干涉儀測量晶片表面厚度的原理,以便即時判斷其研磨製程的終點。
本發明的缺點是研磨墊上所裝置的複數個偵測窗口,其玻璃材質會造成施力條件的不同而影響晶片研磨的平坦度。
圖一、在CMP設備的拋光墊上裝置透明視窗
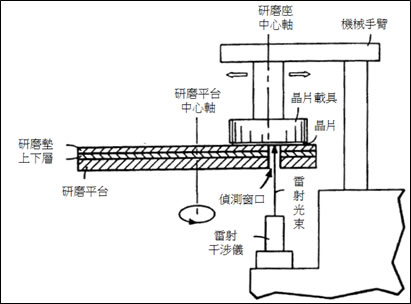
資料來源:USPTO,5893796號專利
該論文的作者利用古典TRIZ的矛盾矩陣求解的過程如下,
| 欲改善的參數 |
不欲惡化的參數 |
發明原則建議 |
| 28.量測精確度 |
31.物體產生之有害作用 |
3,33,26 |
選擇發明原則33.均質性。如圖二所示,筆者推測其原因為偵測窗口的透鏡改用與研磨墊相同特性的材質,同時能避免光學折射或反射作用以確保量測精確度正常,使晶片研磨的平坦度能均勻一致。該專利說明書也指出,研磨墊上所裝置的偵測窗口,其塑化鏡片的材質為聚亞氨酯 (polyurethane),特性與研磨墊相同,可確保晶片研磨後的平坦度能均勻一致。
另外,筆者以為本案例的矛盾配對之邏輯應該修正如下表,理由是「量測精確度」並非已惡化而欲改善之對象,「物體產生之有害作用」才是欲改善之對象。惟其發明原則的選擇結果與前述相同。
| 欲改善的參數 |
不欲惡化的參數 |
發明原則建議 |
| 31.物體產生之有害作用 |
28.量測精確度 |
3,33,26 |
圖二、在CMP設備的拋光墊上裝置透明視窗
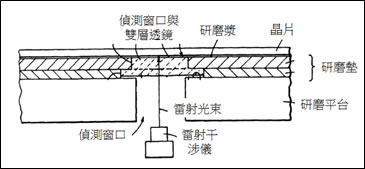
資料來源: USPTO,5893796號專利
其次,該論文作者舉出一個他找不到適用的工程參數之案例如下,專利名稱為”Grooved rollers for a linear chemical mechanical planarization system(線性化學機械平坦化系統的溝槽式傳動軸)”,專利號碼為US6620035。
如圖三所示,該案例敘述一CMP設備在其傳動軸表面製作的平行溝槽可容納殘留的研磨漿與液態物質,其目的是避免因為傳動軸與研磨帶之間壓力分佈不均而影響晶片研磨後的平坦度。
圖三、線性化學機械平坦化系統的溝槽式傳動軸
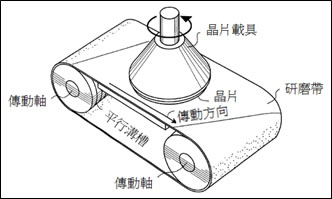
資料來源:USPTO,6620035號專利
依圖四的分析結果,本發明的缺點是傳動軸表面的平行溝槽本身就會導致研磨帶的壓力分佈不均而造成晶片研磨後,平坦度不佳的問題。於是,該論文作者認為本案例找不到適用的工程參數,主張不依照矛盾矩陣求解,並增列新的工程參數「潔淨度」與「均勻度」於下表:
| 欲改善的參數 |
不欲惡化的參數 |
作者自訂的發明原則建議 |
(研磨帶與傳動軸)潔淨度、
(研磨帶)均勻度 |
36.裝置複雜性、
25.時間的損失、
23.物質的損失 |
17.移到新的維度、
15.動態性 |
圖四、線性化學機械平坦化系統的溝槽式傳動軸
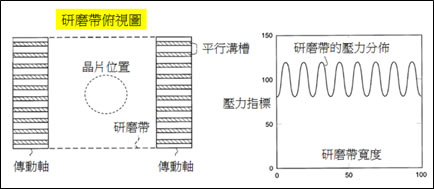
資料來源: USPTO,6620035號專利
不過,筆者認為該案例若利用古典TRIZ的矛盾矩陣即可求解如下,
| 欲改善的參數 |
不欲惡化的參數 |
發明原則建議 |
| 11.應力或壓力 (保持研磨壓力的均勻性) |
12.形狀 (保持晶片研磨後的平坦度) |
35,4,15,10 |
選擇發明原則 4.非對稱性,如圖五所示,將傳動軸的表面改為複數個螺旋狀與橫向溝槽,使殘留的研磨漿容易從交錯式的溝槽之間自動排除至傳動軸外側,進而確保研磨帶的壓力分佈均勻,使晶片研磨後的平坦度回歸正常。
筆者認為本發明的構想與輪胎表面排水用的花紋設計概念相近,可謂是「類比式思考」的成功案例之一。
圖五、線性化學機械平坦化系統的溝槽式傳動軸
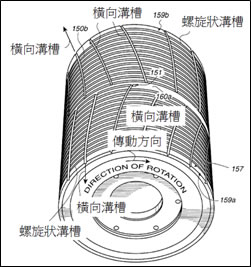
資料來源: USPTO,6620035號專利
下一期專文,筆者將繼續為各位讀者們介紹該論文中,利用TRIZ手法解決CMP技術問題的案例,請大家拭目以待。
 |
|
| 作者: |
胡竹林 |
| 現任: |
北美智權教育訓練處 資深研究員 |
| 經歷: |
高通顯示器 微機電顯示器資深經理
華晶科技 工程部經理
友達光電 資深工程師
加州大學洛杉磯分校 電機研究所碩士 |
|
|

|





