2019年1月7日,USPTO发布了修订版适格性审查基准 (2019 PEG)。USPTO原本期望藉由统整过往判决以建立一套明确的适格性判断流程,讵料在将近10个月中,各界对该修订版本实务适用的建议、乃至于疑惑困扰之处,群情汹涌,排山倒海而至。USPTO因而在搜集各界意见后,针对该等意见发布了「2019年10月美国专利适格性指南更新」(PEG Oct update)。
图片来源:Pixabay
北美智权报曾于《2019年10月美国专利适格性指南更新的五大重点》一文中重点介绍本次更新,本次更新实质内容共17页,其中近8页在探讨抽象概念之分类 (II. The Groupings Of Abstract Ideas Enumerated In The 2019 PEG),这部分的重要性一方面来自于现行判断流程的step 2A中,若能脱逸出列举的抽象概念种类,即可建立申请目标之适格性,不再需要进行step 2A prong two及step 2B审查;另一方面则是因为该等抽象概念种类乃是由USPTO所制定,从业人员必须了解其本质,方能据理对审查意见进行答辩。
概观
Alice一案后,法院采取的作法是将系争请求项与在先案件中已经被认定为抽象概念的请求项进行比较,藉此判断系争请求项是否属于抽象概念。USPTO起初以巡回法院的判决作为比较基础而进行Alice/Mayo 测试,但USPTO很快便发现这样的做法有实际审查上的困难,原因如下:巡回法院已经累积大量的具体个案判决,并据此比较、判断哪些请求目标属于抽象概念,如果审查时也采取法院的案件比较策略,将导致审查效率不合理的下降,更何况,巡回法院的判决仍源源不绝的产生;再者,由于判决是依据个案具体状况产生,导致类似的请求目标在不同案件中有时被认定是抽象概念,有时却反之,令USPTO忧心审查人员及科技中心(Patent Technology Center)进行审查时的一致性。
因此,2019 PEG对抽象概念改采列举的作法,以期提升审查结果的一致性与可预期性:只要落入数学概念 (Mathematical Concepts)、组织人类行为的特定方法 (Certain Methods of Organizing Human Activity) 、心智活动 (Mental Processes) 或暂定的抽象概念 (Tentative Abstract Idea) 其中之一,即属抽象概念。然而,2019 PEG仅提出这些种类,直到PEG Oct update才对抽象概念下所列举的四个种类提供详细的说明与信息,而本刊期将由数学概念开始为读者一一剖析。
数学概念
PEG Oct update中强调,在请求项引述 (recite) 数学概念固然使得请求项落入抽象概念的范畴而不具适格性,惟若一请求项仅只是包含了「基于或涉及数学概念的限缩条件」并不使得该请求项落入抽象概念的范畴。具体而言,只要请求项本身并非引述数学概念,而是以说明书中记载的数学概念作为限缩条件,并不会使得请求项落入抽象概念的范畴。
2019 PEG在数学概念举出了三种子类型,即数学关联性 (mathematical relationship)、数学公式或方程式(mathematical formulas or equation)、数学计算式(mathematical calculation),PEG Oct update虽针对各子类型提出说明,但USPTO仍基于法院判决拒绝细分数学概念的立场,而不愿对这三种子类型做出确切的区别。这其实并不令人意外,因为即便USPTO进行了说明,由于出于相同的本质,上述三种子类型间的分野仍非常模糊,以下是三种子类型的介绍。
● 数学关联性
数学关联性是数学概念的第一种子类型,指的是变量或数字间关系,例如,p=F/A (压力的物理定义),这种关系不限于以数学方式描述,以文字方式描述,例如,压力可以被正向力与受力面积的比例所定义,仍属数学关联性。
PEG Oct update列举了三个在请求项中引述数学关联性的例子,其中有大名鼎鼎的Gottschalk v. Benson,其系争请求项为「二进制编码十进制的数字换算为纯二进制数字的方法」(a conversion between binary-coded decimal and pure binary numerals)就属于引述数学关联性,多数从业人员应可顺利无碍地将2019 PEG及PEG Oct update套用在该系争请求项而得到其引述数学关联性、数学概念的结论。
另外两个例子就较为发人深省了,在Diamond v. Diehr案中,阿瑞尼斯方程式被用来在系争请求项中决定取出产物的最佳时间,PEG Oct update将其编排于数学关联性示例中,显然USPTO认为此种请求项撰写方式不符「基于或涉及数学概念的限缩条件」,而属于引述数学概念,无法直接由step 2A prong one进入PATHWAY B;近期在Mayo及Alice两案中,法院不断重申该案系争请求项具备适格性;加上2019 PEG及PEG Oct update (包括Alice/Mayo 测试) 乃基于近期判决而制定,因此应该符合法院的见解。根据这些间接的迹象,我们仅能得知该系争请求项即便以今日的标准来审视,仍具备适格性,在Alice/Mayo 测试 (见图1) 中最终会进入左下角的终点,但从法院见解或USPTO的审查角度来观察,该系争请求项究竟是由step 2A prong two进入PATHWAY B,抑或经过step 2B而建立适格性,则耐人寻味。
图1. Alice/Mayo 测试流程
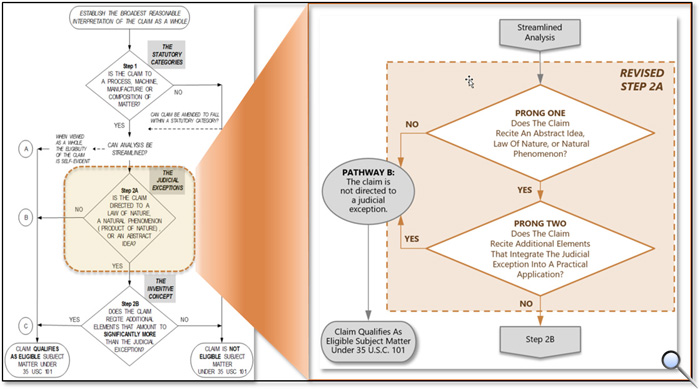
图片来源:October 2019 Update: Subject Matter Eligibility
Mackay Radio & Tel. Co. v. Radio Corp. of Am案则是一场80年前的侵权诉讼,其系争请求项 (第15、16项,见图3) 以电磁学公式及工作波长来界定大型天线数组中导线的长度与夹角 (见图2),虽然该系争请求项最终因为欠缺技术效果而无效 (因此该系争请求项并非有用的结构),但该案判决提出了极为隽永的见解:「尽管科学真理或它的数学表达式不是可专利的发明,但藉助科学真理的知识创建的新颖而有用的结构却可能是可专利『发明』(While a scientific truth, or the mathematical expression of it, is not patentable invention, a novel and useful structure created with the aid of knowledge of scientific truth may be patentable “invention.”)」。USPTO将此系争请求项归类在引述数学关联性的子类型,虽未否定依照科学真理的数学表达式所具体化的物的适格性 (因为仍有step 2A prong two及step 2B之判断步骤),但USPTO显然将依照科学真理的数学表达式所具体化的物,仍视为引述数学关联性。
图2. Mackay Radio & Tel. Co. v. Radio Corp. of Am案的系争专利实施方式之一
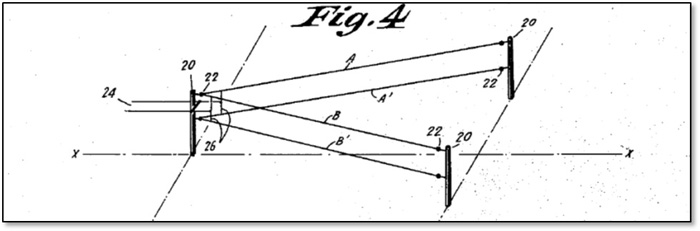
图片来源:美国专利第1,974,384号
图3. Mackay Radio & Tel. Co. v. Radio Corp. of Am案的系争请求项

图片来源:美国专利第1,974,384号
● 数学公式或方程式
引述数值公式或方程式的请求项也被认为属于数学概念的范畴,同样地,以文字方式描述,仍属于这个子类型。USPTO列举了三个例子:Diamond v. Diehr案、Parker v. Flook案及Bilski v. Kappos案,在此有一个现象值得一提。
时序上,Flook案在先而Diehr案在后,两者皆属直接地列举、提出 (set forth) 数学公式或方程式,Flook案的请求项被最高法院判定不具适格性,Diehr案却被认为具备适格性,两案请求项间在性质上的差异非常细微,因此,有论者认为Diehr案推翻了Flook案对适格性的见解。然而最高法院再三论述两案判决的准绳并未变更,Diehr案判决首先提到该案系争请求项并非指向数学演算,而是解决实际问题的制程改进[1],而Flook案的请求项仅是计算警报限值[2],甚至对于如何界定其计算所需之变量的揭露内容也付之阙如[3],Diehr案的请求项则被认定是合成橡胶的固化制程[4],而且Flook案的请求项中无关紧要的post-solution activity (调整警报限值) 对建立适格性无甚帮助[5];于Mayo v. Prometheus案判决中再度对Diehr案提进行阐述,最高法院认定Diehr案的请求项仍为适格,因为除了数学公式以外的其他步骤将该数学公式整合进该制程[6],而且这些步骤使得请求项具备了数学公式以外的意义 ─ 将该制程转化为此一数学公式有进步性的应用[7];Alice v. CLS Bank案判决中,则再度重申Diehr案的请求项虽然使用了「众所周知的」数学方程式,但该数学公式是被于解决「常规工业实务」中的技术问题[8]。
Flook案与 Diehr案同时出现在本次数值公式或方程式的案例中证明是否引述数学概念未必对请求项适格性产生决定性影响,然而更重要的是,此二案件是最高法院所生成为数不多的同类型正反案件对比,时至今日最高法院仍维持一贯的见解,认定此二案件的请求项确实有所区别。对于第一线从业人员而言,此二案件的重要性应在于透过历次判决所指出的细微差异去揣摩与感受此二案件请求项的区别,进而在撰写类似案件时将申请案的风格与架构往Diehr案请求项靠拢。
● 数学计算
数学计算是最后一个数学概念的子类型,在此的数学计算指的是运算 ─ 例如乘法,或是利用数学方法决定变量或数值的计算行为 ─ 例如求幂的算术运算。在撰写请求项时需要特别注意的是,就说明书的角度而言且在最宽广合理解释的原则下,请求项除了直接记载「计算」(calculating) 会被认定落入该子类型,只要记载藉由数学方法进行「决定、判断」(determining)、「执行」(performing) 等步骤、行为,均会被认为该子类型所涵盖。
于此,USPTO提供了三个例子,其中以SAP Am., Inc. v. InvestPic, LLC案及Burnett v. Panasonic Corp.案较不为人所知。
在InvestPic案中,专利权人 (InvestPic, LLC) 指出传统的金融信息网站基于历史信息统计所提供的预测讯息对用户用处不大,因为其依赖基于正态分布[9]的机率分布方程式,但现实中金融市场的数据往往符合重尾分布[10],因此提出一种再取样的统计分析方式,以改善预测讯息准确度,稍有经验专利工程师若是听取完这样的解决方案想必心中已经警铃大作,其请求项1具体如下:
1. A method for calculating, analyzing and displaying investment data comprising the steps of:
(a) selecting a sample space, wherein the sample space includes at least one investment data sample;
(b) generating a distribution function using a re-sampled statistical method and a bias parameter, wherein the bias parameter determines a degree of randomness in a resampling process; and,
(c) generating a plot of the distribution function.
上述黑体字显示,触发该子类型认定的用字预估比PEG Oct update内文直接提供的用字还要广泛得多。但InvestPic案毕竟涉及商业方法,被认定引述数学运算并不令人意外,然而Panasonic案则揭示了涉及处理信息的装置是如何被认定为引述数学运算,其请求项1如下:
1. A geospatial media recorder, comprising:
converting means for converting longitude and latitude geographic degree, minutes, and seconds (DMS) coordinate alphanumeric representations or decimal equivalent geographic coordinate alphanumeric representations and altitude alphanumeric representations into individual discrete all-natural number geographic coordinate and measurement representations; and
combining means for concatenating the individual discrete all-natural number geographic coordinate and measurement representations into a single discrete all-natural number geospatial coordinate measurement representation for identification of a geospatial positional location at, below, or above earth’s surface allowing user to geospatially reference entities or objects based on the identified geospatial positional location and point identification.
判决中具体阐述了巡回法院认定该请求项引述数学运算的逻辑:
将经、纬度转换 (converting) 为自然数 ─ 移去小数点,并把所有的「+」、「–」分别以1与0取代;把该自然数串接 (concatenating) ─ 接合经、纬度形成的自然数形成一串自然数,以上简言之就是将地理坐标转换为一串自然数。专利权人 (Burnett) 主张此处的串接应解释为编写过程 (programming process),法院并不认同,因为请求项的核心仍是抽象概念,即便接受专利权人的说词,根据判决先例,一方法过程,以信息始,施以算法,终结于该信息的新格式,仍属抽象概念[11]。
小结
这次PEG Oct update中,USPTO或明示、或暗示地传达了在面对数学概念时心中的那把尺:首先,虽然这类型案例不多,但若装置项中各组件配置、相对关系是直接引述自然科学的公式 ─ 将数学关联性具体化,该装置仍属引述数学概念;堪以告慰的是,透过Flook案与Diehr案的成对出现,可以揣测USPTO可能意图传达「引述数学概念的请求项并非无路可走」的见解;更重要的是,透过发掘案例的详细内容,则可以判断引述数学概念并非仅取决于请求项的用字 (wording),而需要参酌说明书内容,进而探求请求项所提出技术方案的真意。
备注:
- Diamond v. Diehr, 450 U.S. 175, 181 (1981), “The respondents' claims were not directed to a mathematical algorithm or an improved method of calculation but rather recited an improved process for molding rubber articles by solving a practical problem which had risen in the molding of rubber products.”
- Id., at 186, ‘The claims were drawn to a method for computing an “alarm limit.”’
- Id., “The application, however, did not purport to explain how these other variables were to be determined nor…”
- Id., at 187, “In contrast, the respondents here do not seek to patent a mathematical formula. Instead, they seek patent protection for a process of curing synthetic rubber.”
- Id., at 191, “Similarly, insignificant postsolution activity will not transform an unpatentable principle into a patentable process.”
- Mayo v. Prometheus, 566 U.S. 66, 80 (2012), “…because of the way the additional steps of the process integrated the equation into the process as a whole.”
- Id., at 81, “These other steps apparently added …—they transformed the process into an inventive application of the formula.”
- Alice v. CLS, 573 U.S. 208, 223 (2014), ‘The claim employed a “wellknown” mathematical equation, but it used that equation in a process designed to solve a technological problem in “conventional industry practice.”’
- Normal distribution or Gaussian distribution,早期我国教育体系多称其为常态分布,但讽刺的是正态分布在现实生活中极为罕见,绝非常态。
- 一种在自然界更为常见的机率分布形式,具体以少量个体做出大量贡献或占用大量资源的样貌呈现。
- Digitech Image Techs., LLC v. Elecs. for Imaging, Inc., 758 F.3d 1344, 1351 (2014)
好消息~北美智权报有微信公众号了!
《北美智权报》内容涵盖世界各国的知识产权新闻、重要的侵权诉讼案例分析、法规解析,以及产业与技术新知等等。
立即关注北美智权微信公众号→ NAIP_IPServices
~欢迎读者分享与转发~ |
 |
|
| 作者: |
喻韬 |
| 現任: |
北美智权专利工程部专利工程研究组研究员 |
| 经历: |
台湾知名法律事务所专利工程师 |
| 学历: |
东吴法硕乙法律专业组
(台湾地区)台科大专利所硕士、(台湾地区)清华大学生资所硕士
(台湾地区)北科大电子系学士、(台湾地区)东华大学生科系学士 |
| 专长: |
专利申请 (布局、撰稿、答辩);欧盟、美国、中国、台湾专利法规及相关判例研究;台湾专利 举发及诉讼 |
|
|
|

